合わせ鏡をのぞいてみると
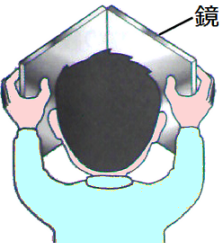
1枚の平面鏡に自分の顔を映すと、頭は鏡の上側、あごは鏡の下側、左目は鏡の左側、右目は鏡の右側に映ります。それでは次の図のように2枚の平面鏡を直角につないだ合わせ鏡をのぞきこむと自分の顔はどのように映るでしょうか。
この場合、頭は鏡の上側、あごは鏡の下側に映りますが、左目は鏡の右側に、右目は鏡の左側に映ります。試しに右眼をウインクしてみると、鏡の左側に映った目がウインクします。これは顔の左側が鏡の右側に、顔の右側が鏡の左側に映るからです。
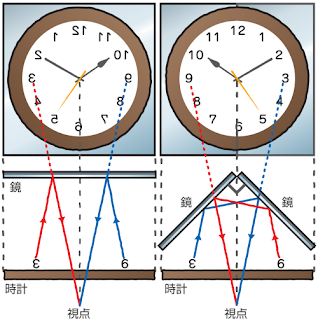
このとき光はどのような道筋を進んでいるのでしょうか。鏡に映すものを時計にして考えてみましょう。次の図の左側のように平面鏡の前に時計を置いて時計の真後ろから鏡をのぞくと文字盤がひっくり返った時計が映ります。このときの光の進み方を赤と青で示しました。光の反射の法則に従って一枚の鏡の中に時計の虚像が見えていることがわかります。
右側のように2枚の平面鏡を直角に合わせ、鏡の接合面が中心になるように時計を置いて鏡の真後ろから鏡をのぞくと文字盤がひっくり返っていない時計が映ります。これは時計の左側から出た光が左側の鏡で反射し右側の鏡の中に映り、時計の右側から出た光が右側の鏡で反射し左側の鏡の中に映って見えるからです。2枚の鏡の中の虚像を全体として見ると文字盤がひっくり返っていない時計になります。
合わせ鏡で見える虚像の数
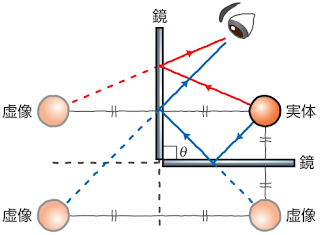
次の図のように90度の合わせ鏡の前に物体を置いてのぞき込むと鏡の中に物体の虚像が3つ見えます。
ここで鏡を合わせる角度を変えると見える虚像の数も変わります。合わせ鏡の角度をθとすると、見える虚像の数は次の式のようになります。光の直進性と光の反射の法則によって、鏡の角度と虚像の数が規則的な関係になるのです。たとえば60度では5個、30度では11個の虚像が見えます。
\[ 虚像の数=\mid \frac{360}{ \theta} - 1 \mid \]【関連記事】

0 件のコメント:
コメントを投稿